What is A Proportional Relationship?

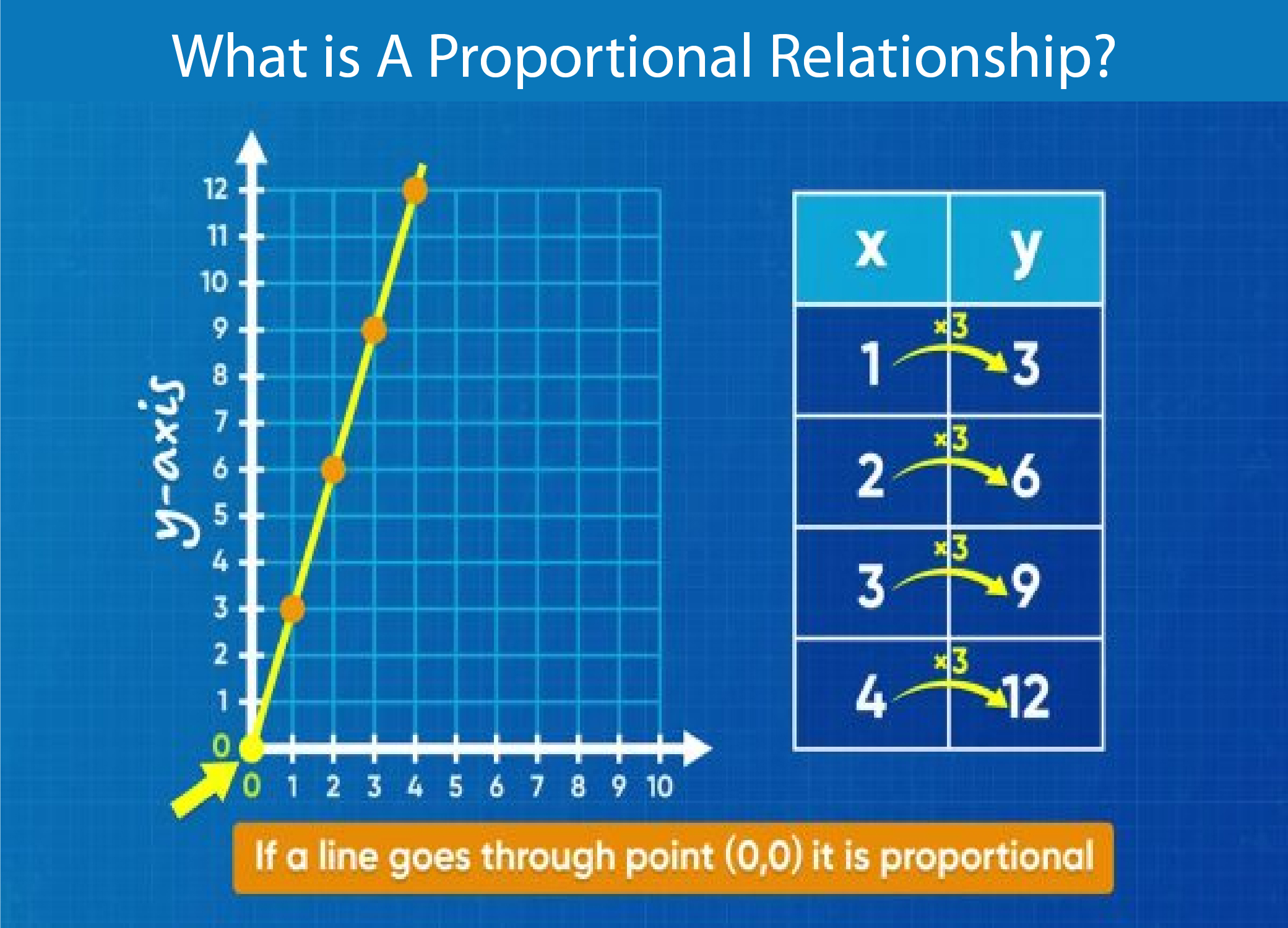
A proportional relationship is a type of mathematical relationship in which two variables are directly proportional to each other. This means that if one variable increases, the other variable increases at the same rate, and if one variable decreases, the other variable decreases at the same rate. The relationship can be represented by the equation y = kx, where y and x are the two variables and k is the constant of proportionality.

Here’s An Example Of A Parabola

A parabola is a symmetric, U-shaped curve defined by the equation y = ax^2 + bx + c, where a, b, and c are constants.

Example: The equation y = -2x^2 + 4x – 3 represents a parabola. The graph of this equation is a parabola that opens downward and has a vertex of (-0.5, -2.75)

You can also plot this parabola on a graph by finding the value of y for several different values of x and then plotting those coordinates on the graph. The set of all points that are the solutions of this equation form the parabola.

What is A Proportion?

Let’s Take A Look at An Example of What is A Relationship Between Two Quantities

One example of a relationship between two quantities is the relationship between speed and time. The speed of an object is defined as the distance it travels divided by the time it takes to travel that distance. This relationship can be represented by the equation:

Speed = Distance/Time

For example, if a car travels a distance of 100 miles in 2 hours, its speed can be calculated by dividing the distance by the time:

Speed = 100 miles / 2 hours = 50 miles per hour

This relationship shows that as the time to travel a certain distance increases, the speed at which the distance is covered decreases, and vice versa. This relationship holds true for any object moving at a constant speed over a certain distance.

Another example is the relationship between force and acceleration. The force applied to an object is equal to its mass multiplied by its acceleration. This relationship can be represented by the equation:

F = m * a

where F is the force, m is the mass, and a is the acceleration. This relationship shows that as the force applied to an object increases, its acceleration increases, and as the force decreases, the acceleration decreases.

Graphs of These Sorts are Called Linear Equations

The relationship between two quantities that result in a straight line on a graph is called a linear equation. A linear equation can be represented in the form of y = mx + b, where y and x are the two quantities being related, m is the slope of the line, and b is the y-intercept, the point at which the line crosses the y-axis.

Linear equations can be used to model real-world situations where the relationship between two variables is directly proportional. Some examples of linear equations include:

• The relationship between distance and time traveled at a constant speed.
• The relationship between temperature and heat added or removed.
• The relationship between price and quantity of a good in a market.

Linear equations are used widely in physics, economics, engineering, and many other fields for modeling real-world phenomena. The slope of the line (m) represents the rate of change of one variable with respect to the other, and the y-intercept (b) represents the value of the dependent variable when the independent variable is zero.

A Great Example of What is A Proportional Relationship Can Be Found in Physics

A proportional relationship can be found in many areas of physics, as many physical phenomena can be described using mathematical relationships between different quantities. One example of a proportional relationship in physics is the relationship between force, mass, and acceleration. According to Newton’s Second Law of Motion, the force acting on an object is equal to the mass of the object multiplied by its acceleration. This relationship can be represented by the equation:

F = m * a

where F is the force, m is the mass, and a is the acceleration. This equation shows that the force applied to an object is directly proportional to its mass and its acceleration.

For example, let’s say you have two objects: Object A has a mass of 10 kg and Object B has a mass of 20 kg. If you apply the same force of 100 N on both objects, the acceleration of Object A will be 10 m/s^2 (F=ma) and Object B will have an acceleration of 5 m/s^2. As you can see the relationship between force, mass and acceleration is directly proportional.

Another example of a proportional relationship in physics is the relationship between the period and the length of a simple pendulum. The period, or the time it takes for a pendulum to complete one full swing, is directly proportional to the square root of the length of the pendulum. This relationship can be represented by the equation:

T = 2π * √(L/g)

where T is the period, L is the length of the pendulum, and g is the acceleration due to gravity. This equation shows that as the length of the pendulum increases, the period of the pendulum also increases.

In general, proportional relationship is a common way to describe physical systems, and these examples are just a few examples of the many ways in which proportional relationships can be found in physics.

We Can Express This Relationship in A More Mathematically Accurate Way

The relationship between force, mass, and acceleration can be expressed in a more mathematically accurate way by using vector notation. In vector notation, force is represented by the vector F, mass is represented by the scalar m, and acceleration is represented by the vector a. The relationship between these three quantities can be represented by the vector equation:

F = m * a

This equation states that the force vector (F) is equal to the product of the scalar mass (m) and the acceleration vector (a). This equation is mathematically equivalent to the scalar equation F = m * a, but it gives more information about the direction of the force and the acceleration.

Another way to express this relationship more mathematically accurately is by using the concept of the net force. In physics, the net force is the overall force acting on an object, taking into account all the forces acting on it from different directions. The net force is the vector sum of all the forces acting on an object. The net force vector F_net is given by:

F_net = F1 + F2 + F3 +…

Where F1, F2, F3 are the different forces acting on the object.

In summary, the relationship between force, mass, and acceleration can be more mathematically accurate by using vector notation and the concept of the net force. This allows for a more precise understanding of the direction and the magnitude of the forces acting on an object and the resulting acceleration.

What Does This All Mean For Us?

The relationship between force, mass, and acceleration are important for us in many ways. It helps us understand the motion of objects and the forces that act on them, which is fundamental for many fields such as physics, engineering, and everyday life.

In engineering, understanding this relationship is crucial for designing structures, vehicles, and machines that can withstand different forces and perform specific tasks. Engineers use this relationship to calculate the forces that different structures and machines need to withstand and to design them accordingly.

In transportation, Newton’s second law is used to determine the force required to accelerate a vehicle to a certain speed and to stop it, which is important for designing cars and airplanes that are safe and efficient.

In sports, the principles of force, mass, and acceleration are used to improve performance. Athletes use this relationship to increase their speed and power by training to increase their muscle mass and to improve their acceleration.

In everyday life, the relationship between force, mass, and acceleration can be observed in many situations. For example, when you push or pull an object, the harder you push or pull, the faster it moves or the more it accelerates. This relationship is also important for understanding how objects fall to the ground and how to keep them from falling.

In summary, the relationship between force, mass, and acceleration is a fundamental concept. That helps us understand how physical systems behave and have a wide range of applications in engineering, transportation, sports, and everyday life. It allows us to predict and control the motion of objects, which is important for safety, efficiency, and performance.

Also Read: What is Classified Balance Sheet